Suppose you have decided on a suitable model for a timeseries. In this case, we have selected an ARIMA(2,1,3) model, using the Akaike Information Criteria (AIC) as our sole criterion for choosing between various models here, where we model the DJIA.
Note: There are many criteria for choosing a model, and the AIC is only one of them. Thus, the AIC should be used heuristically, in conjunction with t-tests and the Coefficient of Determination, among other statistics. Nonetheless, let us assume that we ran all these tests, and were still satisfied with ARIMA(2,1,3).
An ARIMA(2,1,3) looks like this:
This is not very informative for forecasting future reaizations of a timeseries, because we need to know the values of the coefficients ,
, etcetera. So we use R’s arima() function, which spits out the following output:

Thus, we revise our model to:
Then, we can forecast the next, say 20, realizations of the DJIA, to produce a forecast plot. We are forecasting values for January 1st 1990 to January 26th 1990, dates for which we have the real values. So, we can overlay these values on our forecast plot:
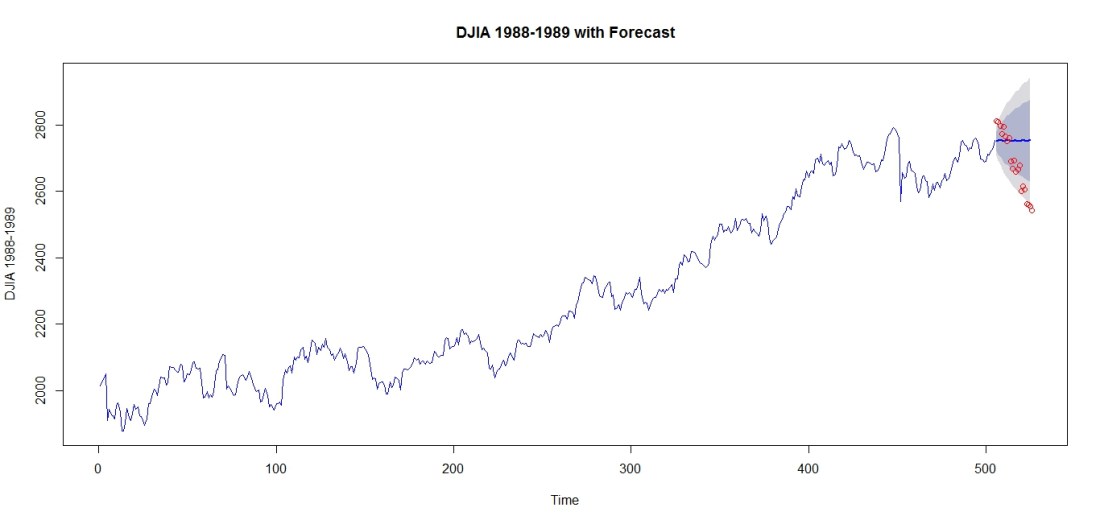
Note that the forecast is more accurate for predicting the DJIA a few days ahead than later dates. This could be due to:
- the model we use
- fundamental market movements that could not be forecasted
Which is why data in a vacuum is always pleasant to work with. Next: Data in a vacuum. I will look at data from the biggest vacuum of all – space.
Hello!
I really like your post. I am working currently on a project and i have a issue . I chose the right parameters by doing a great code on python,finding the right period of training also. But the ting is that I don’t know which time series to run with ARIMA method. The differenciated time series or the original one. Do I need to implement the equation or I have just to call it from my libraries.
Thanks anyway!
I really like your blog
Hi SARR! Thanks for the praise.
You should run a stationary time series. First, check if the original timeseries is stationary (by simple timeseries plot, ACF), and if it is, you can fit an ARIMA to it. See https://coolstatsblog.wordpress.com/2013/08/14/using-aic-to-test-arima-models-2/ for more info.
If the ts is not stationary, difference it, and test the differenced series for stationarity. Keep repeating this until you attain a stationary series, and run an ARIMA model past that.
Hope this helped.
Abbas
Hi,
If I have understand, if the the acf shows that the ts is not stationary we difference it once then we plot the acf again until obtaining stationarity.
I want to know if there is a possibility to decide from a ts plot if it is an arima or arma model
how the aic creterion is calculated, is there any others criterion, if so which one is more used
if we have a seasonal data, how to introduce this seasolnality Sarima(p,d,q)s in R and how to choose s.
thank you
Thanks for your quick answer Abbas. So, if I understand well in my case for exemple:
-The original time series is not stationary was not stationary at the begining after testing its stationarity
-Then I did a first differenciation and test for stationarity, and it was.
-then i did a combination of 36 possible cases for ARMA parameters of the first order time series
-And after choosing the one with the first AIC
I tried to fit an ARIMA of the original time series but my prediction looks like a trend (straight line ax+b form).
I do not get where my mistake is.
I am really sorry to bother,I am just stucked. And up to now this blog helped me a lot.
Can you be more clear on the ARIMA time series to fit: the original or the 1rst order diff ? what about my prediction?
Sorry for my english, I am not a native (from Senegal)
Excus me for my previous post here I did some corrections:
“Thanks for your quick answer Abbas. So, if I understand well; in my case for exemple:
-The original time series was not stationary at the begining
-So I did a first differenciation and test for stationarity, and it was at first order of differenciation.
-then i did a combination of 36 possible cases for ARMA parameters of the first order time series
-And after choosing the one with the first AIC
-I tried to fit an ARIMA of the original time series but my prediction looks like a trend (straight line y= -ax+b form) however my original time series is the evoution of the windspeed in a wind park.My forecast is really not expected
I do not get where my mistake is.
I am really sorry to bother you,I am just stucked. And up to now this blog helped me a lot.
Can you be more clear on the ARIMA time series to fit: the original or the 1rst order diff ? what about my prediction?
Sorry for my english, I am not a native (from Senegal)
Hi SARR, an ARMA(p,q) is the same as an ARIMA(p,0,q).
Once you have a stationary series, fit an ARMA(p,q) or ARIMA(p,0,q) to the stationary one (so, the first or second difference series). In either case, you basically need to deduce p and q. Methods to do so:
a) Run multiple ARMAs and pick the lowest AIC.
b) If you are using R, install the “forecast” package, and simple run auto.arima(x), where x is your timeseries. It will tell you the ARIMA
No worries, your English is excellent.
Hi Abbas,
Thank you for your wonderful blog. Your posts were very instructive for me.
I currently working on my MATLAB project and I want to forecast wind speed for next 24 hours with ARIMA method.
can you give me a hint that how can I find the best values for arima p, d and q parameters? I will be so thankful if you introduce me to a brief and easy to understand reference.
Thank you very much for your help in advance.
Thank you for the kind words, mrezamrt. I’m afraid I do not use Matlab. If you consider using R (faster and more powerful), you can use the auto.arima function to find p, q, r.
Excellent way of describing, and pleasant paragraph to get information concerning my presentation topic, which i am going to present in university.
Glad. Thanks Lavonne!
Hi, really like your post. Especially for the explanation of ARIMA forecast. Where to you find the description for the light and dark gray region in the plot? I googled to get nothing until I saw your post.